S Function Simulink Cstr Continuous Stirred Tank Heater

In Chemical Process Industries (CPI) we use continuous stirred tank reactor (CSTR) or mixed flow reactors for various product manufacturing. For instance, we can use these reactors for liquid-liquid, liquid-gas, liquid-liquid-solid and liquid-gas-solid phase reactions. Moreover, a fluidized bed reactor is also a CSTR where gas-solid phase reaction occurs. In this article we will develop a mathematical model for an exothermic CSTR.

So, to develop this model we will consider an example of Propylene Glycol production. This reaction is a liquid phase and is exothermic in nature. Moreover, we assume that reactor mass is perfectly mixed. In other words, product stream composition and temperature are same as inside the reactor. Remaining CSTR details are as below.

• System Description
• Material Balance of the CSTR
• Heat Balance for CSTR
• Continuous Stirred Tank Reactor Model for Steady State Condition
• Results of CSTR Model
• Conclusion

System Description

In this example, to produce propylene glycol we are doing hydrolysis of propylene oxide. Below is chemical reaction for your reference.

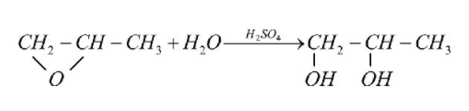
Above reaction is very fast and takes place at room temperature (i.e., 25 – 34 ⁰C). This happens at atmospheric pressure and we use sulfuric acid as a catalyst. For sake of easiness let us designate propylene oxide as D, water as S and propylene glycol as R, now we can represent above reaction in simplified form as D + S = R.

From available literature, Furosawa et al. state that under above reaction conditions, this is a first order reaction based on propylene oxide concentration as below:

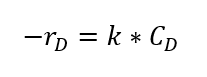
C_D is the concentration of propylene oxide, and equilibrium constant is as follows,

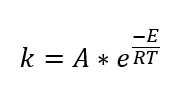
Here, E = 32400 Btu/lb mol and A = 16.96 x 10¹²

To understand the process, we can refer below figure. In this CSTR we feed propylene oxide with water and methanol. Here we add methanol as a diluent, because propylene oxide is not soluble in water. To remove the heat of reaction we use cooling water circulation in reactor jacket.

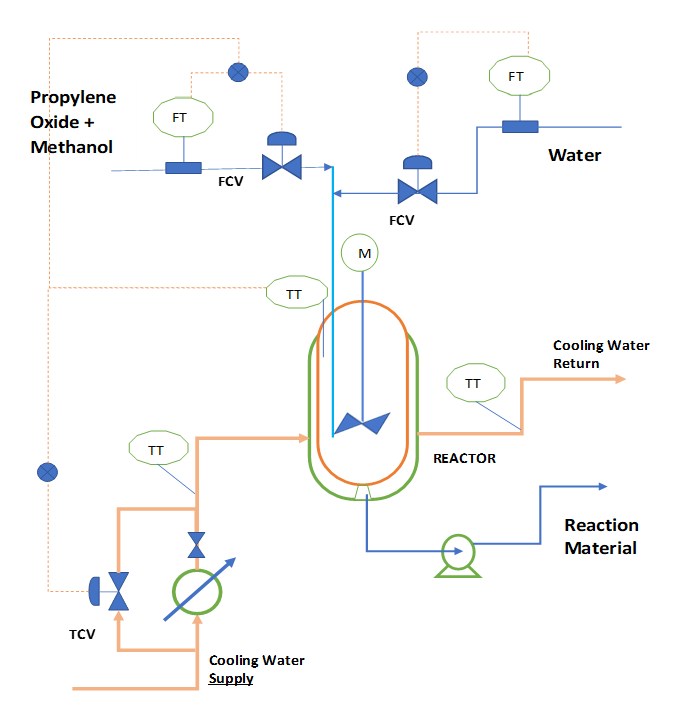
Material Balance of the CSTR

So, we can write the mass balance for raw material D (polypropylene oxide) as bellow:

Rate of D in feed – Rate of D in product – Rate of D reacting = Rate of accumulation/depletion of D in reactor

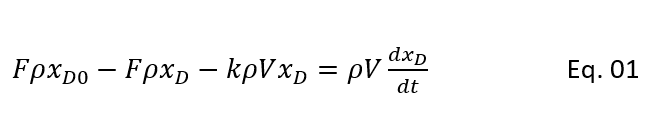
(Rate of D reacting, -V*r_D = V*dC_D/dt = k*V*C_D, since V*C_D = ρ*V*x_D , hence C_D = ρ*x_D . Hence, we can right -V*r_D = ρ*V*dx_D/dt = k*V*ρ*x_D )

Here,     F = feed rate (ft³/h)

              x_D0 = mole fraction of propylene oxide in feed

              x_D = mole fraction of propylene oxide in reactor

              ρ = density of reacting mixture, (moles/ft³)

              V = volume of reacting mixture (ft³)

Heat Balance for CSTR

So, for a CSTR we can write heat balance as follows:

Heat in with feed – Heat out with product + Heat generation during reaction – Heat removed in reactor jacket = rate of heat accumulation/depletion in reactor

So, we get as below equation,

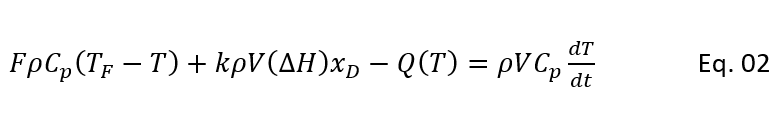
Where, T_F = feed stream temperature (⁰F)

              T = reactor temperature, which is product temperature also (⁰F)

              Cp = specific heat of mixture inside the reactor (Btu/lb mol⁰F)

              Q(T) = Heat removed through reactor cooling jacket (Btu/h)

              ∆H = heat of reaction (Btu/lb mol of D reacted)

 In writing above both equation we have assumed that,

• Flow rates of reactor input and output are equal and constant.
• Reaction mass inside the reactor is in perfectly mixed condition. So, this ensure that concentration and temperature of reactor outlet stream are same as inside the reactor.
• Specific heat of the reacting mixture is constant and independent with the conversion of propylene oxide.
• The heat of reaction is constant and the change with reactor temperature and conversion is negligible.

Continuous Stirred Tank Reactor Model for Steady State Condition

So, we can see above equation 1 and 2 are time dependent and relevant for start-up conditions. Because start-up process is an unsteady state operation and remain time dependent till it reaches at steady state operation. Once CSTR is at steady state condition this change with respect to time will be zero. To get the relation between x_D and T, divide the equation 1 by 2, we get below relationship.

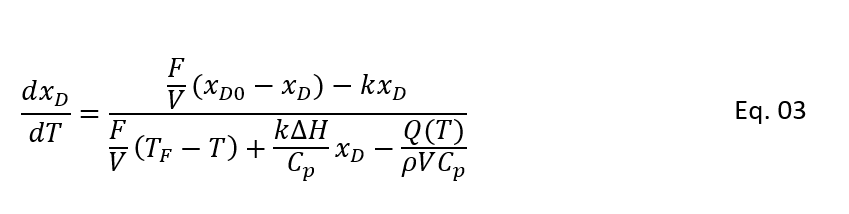
In above equation we have eliminated the time (t) and this is a differential equation between x_D and T. As we discussed above, for steady state there is no change in reactor concentration and temperature with time. So, we can simplify Eq. 1 and 2 as follows:

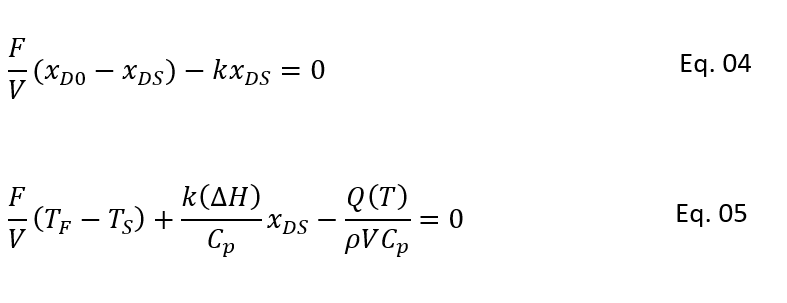
Here, x_Ds and T_s are the steady state values for x_D and T

So, to get relationship between steady state conversion and temperature we can rearrange the equation 4 as below.

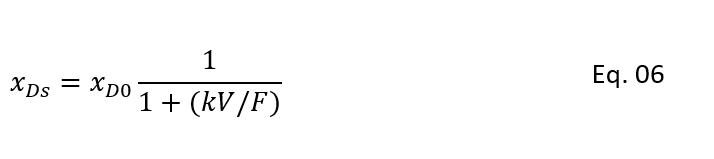
Moreover, after estimating heat removal rate from the CSTR cooling jacket. We can put this in equation 5 and can solve for x_DSE as below. In below equation x_DSE is the concentration which satisfy the CSTR energy balance (i.e., heat generation rate = heat removal rate):

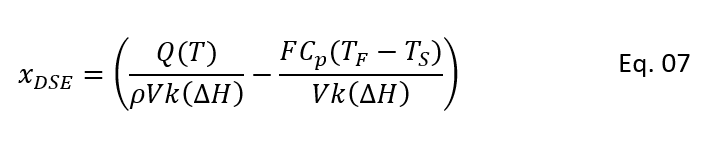
Results of CSTR Model

Now to solve above equation 6 and 7 we need numerical values of various parameters. For this purpose, we will consider the example 8-4 given for a continuous stirred tank reactor in CHEMICAL REACTION ENGINEERING (H. SCOTT FOGLER).

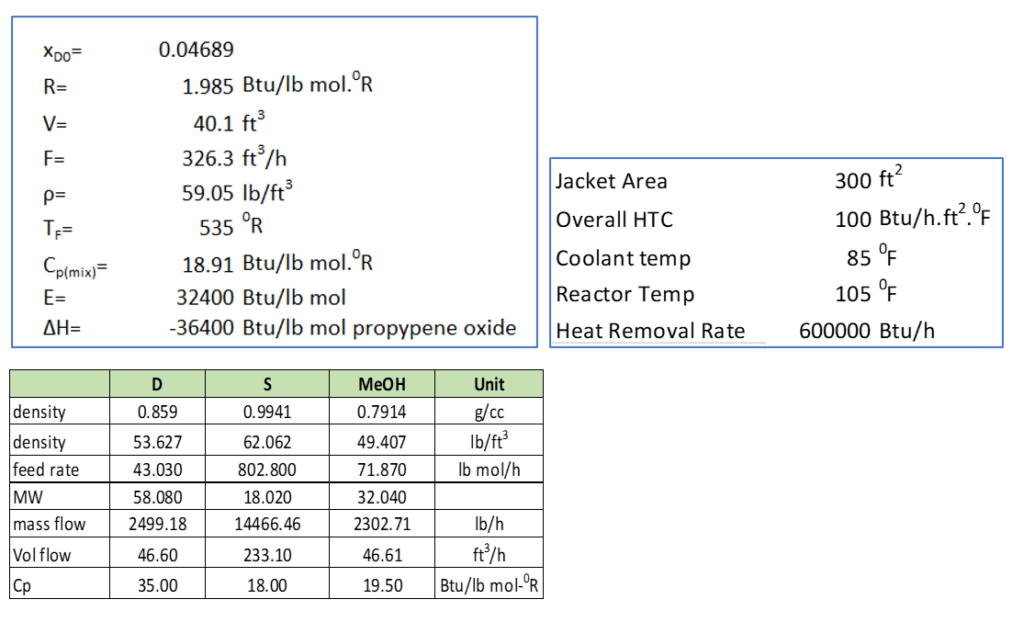
And, rate constant is,

k = 16.96 x 10¹² (e^-32400/RT) h^-1

here unit of E is -32400 Btu/lb mol.

In this example, the feed stream consists an equi-volumetric mixture of propylene oxide (46.62 ft³/h) and methanol (46.62 ft³/h). And, water flow rate is 233.1 ft³/h, which contains 0.1 wt.% H₂SO₄ as catalyst.

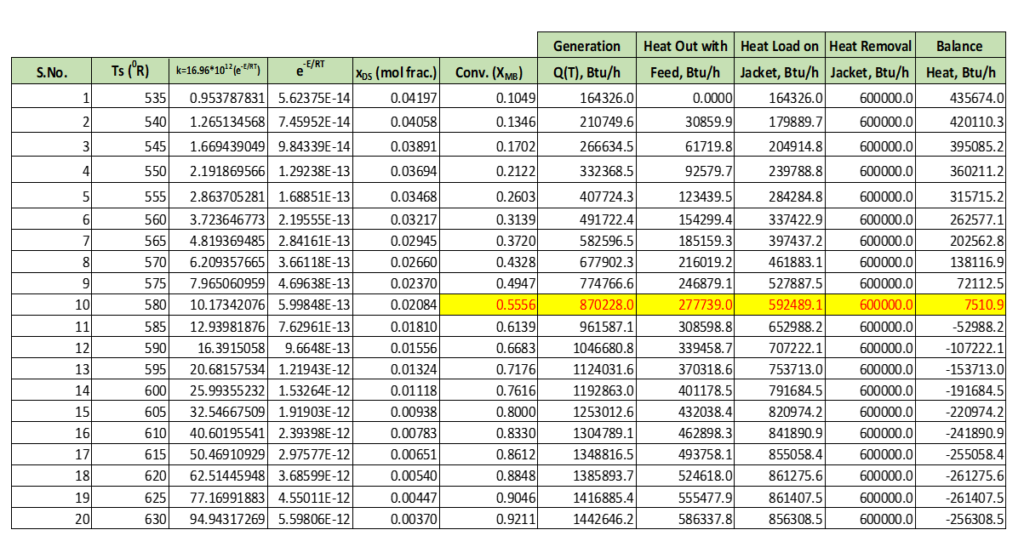
In below table we can see the calculation results for steady state temperature, conversion and heat generation for the reaction. We can see in yellow highlighted cell at steady state temperature T_s = 580 ⁰R, propylene oxide conversion is X_MB = 55.56%. Which is maximum which we can achieve from this reactor. Because heat removal rate is limiting which is 600000 Btu/h as given in above table in right hand. After T_s = 580 ⁰R, heat generation rate become higher than rate of heat removal from cooling jacket.

However, we can operate this reactor next steady states level also which are higher operating temperature levels. Which we can see in below table also.

Below figure talks about change in conversion with reactor temperature.

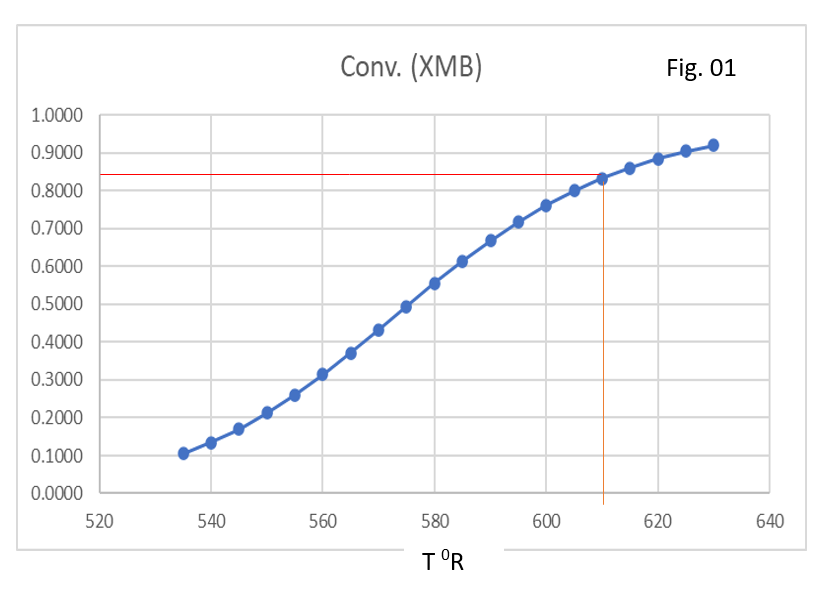
Similarly, we can solve equation 7 which will give us the value of x_DSE, which is steady state concentration of propylene oxide in reactor. At this concentration heat removal rate should be equal to the heat generation rate. Below, figure shows beyond 620 ⁰R, there will be run away for given reactor system.

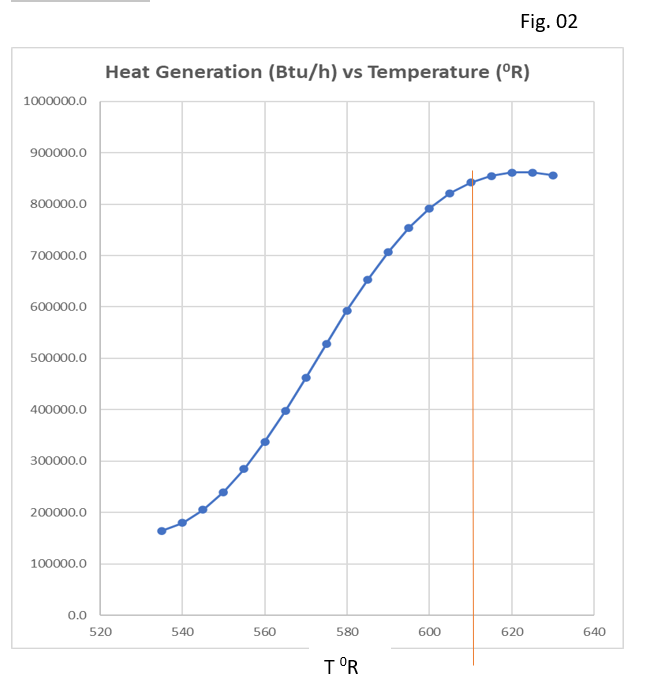
For designing, a continuous stirred tank reactor system we should use Fig-01 and Fig-02 simultaneously. Here, we can see clearly for given heat removal capacity of the reactor (which is here 600000 Btu/h). The max safe operating temperature is 610 ⁰R. Therefore, it is recommended to operate this reactor around 580 ⁰R.

For given system max possible conversion we can achieve is 84% approximately at 610 ⁰R.

Conclusion

So, in this article we developed mathematical model for a non-isothermal continuous stirred tank reactor (CSTR). We can use these equations to find out max possible conversion at adiabatic and isothermal conditions. In case of adiabatic conditions reactor conversion is limited by max allowable reactor temperature. After which reaction can lead to run away conditions. While, in case of isothermal reactor we can maintain the reactor temperature by using cooling coil, cooling jacket or a circulation cooler. This way we can afford to achieve higher reactor conversions.

Thanks for reading and welcome your feedbacks.

rogersweandstaid.blogspot.com

Source: https://www.chemengghelp.com/continuous-stirred-tank-reactor/

Share this post